The Hydrino Hypothesis Chapter 4
An Introduction To The Grand Unified Theory Of Classical Physics
This monograph is an introduction to Randell L. Mills’ Grand Unified Theory of Classical Physics, Hydrino science, and the efforts of the company Brilliant Light Power (BLP) to commercialize Hydrino-based power technology, as told by Professor Jonathan Phillips. Out of necessity, it assumes a degree of familiarity with physics and physics history. An overview of the BLP story which serves as a helpful introductory piece to those unfamiliar with its sweeping scope can be found here. Readers should also read the previous chapters of this monograph prior to this one:
Chapter 1 of The Hydrino Hypothesis
Chapter 2 of The Hydrino Hypothesis
Chapter 3 of The Hydrino Hypothesis
By Professor Jonathan Phillips
Applying The GUTCP & SQM To Atoms
Preface- This is the first mathematical chapter. It is a good place for folks trained in SQM and narrowly focused on a mathematical argument supporting the GUTCP to start. This chapter repeats many of the arguments made in Chapter 3, but with detailed mathematics. No more bunny slope, now you take a real chair lift and follow your instructor down a challenging piste. The finale is the demonstration that only the GUTCP provides a solid, simple method for predicting the energy levels of atomic systems with more than one electron. In other words, it is shown that the GUTCP, employing only classical physics and not a single post-1872 equation or variable parameters, predicts atomic spectra. In contrast, beyond hydrogen nothing is predicted using SQM, not even the helium spectra. Remember as you read that “everyone knows” is not a scientific argument.
Introduction
Contrasting the mathematics and physical models of the GUTCP and SQM as applied to atoms assists in highlighting the differences between these distinctly different paradigms of quantum physics.
In sum, bottom-line-up-front (BLUF), the following review shows that the GUTCP is based entirely on the postulate that elementary particles are physical objects of distinct shape that obey classical physics equations, that is equations postulated before 1872.12 This is in contrast to the SQM model which assumes elementary particles are infinitely small, that is non-physical objects, that do not obey the laws of classical physics (e.g. reject Newtonian mechanics), but can only be described as existing with some probability at a point and a time, as defined by the solutions to an equation, Schrodinger’s equation, first postulated in 1925.
Consider the GUTCP model applied to atoms in the ground state/lowest energy non-Hydrino state first (in a later chapter excited states will be visited). Only two fundamental equations are employed to predict the spectroscopy of atoms.3 The first is the same equation, a Newtonian force balance, used to determine the movement of the planets, and the relation between orbital height and velocity, information needed to launch satellites. First fundamental equation:
For satellites, the only central force is the gravitational pull of earth:
Thus, for example, if one knows the intended distance a satellite is to orbit from earth center (r), Eq. 4-1 permits the determination of the velocity (v) of the satellite required to make the orbit stable. The other values, G, the gravitational constant, me, the mass of earth and ms, the mass of satellite are simply constants.
Notably, there is a continuum of solutions to this single equation. A satellite, for example, can be at any altitude, once the velocity is adjusted.
The second fundamental equation employed in the GUTCP is also simple and classical. It is the conservation of angular momentum. For electrons the angular momentum is a MEASURED value: h-bar, known as Plank’s constant. The value of h-bar is set on the basis of experimental determination.
The next unique feature of the GUTCP model of significance is the proposed physical structure of the bound electrons. Specifically, it is postulated the electron is a spherical shaped 3-D object, an “orbitsphere” in the nomenclature of the GUTCP, that is an actual physical spherical bubble of mass and charge, with specific, great circle shaped surface currents that symmetrically surrounds the nucleus of the atom, as seen in Figure 4-1 below. It has a thickness, the gravitational thickness, described elsewhere (Ref. 4-3).
Figure 4-1: Orbitsphere, the GUTCP model of the electron.
The orbitsphere is not the first attempt to imagine the electron as a physical object that obeys classical physics laws. Over the last one hundred plus years, there have been many efforts to mathematically describe bound electrons as physical objects. However, in all prior, and failed, efforts, the electron was modeled as a small particle (of indeterminant size) orbiting a very small nucleus containing neutrons and protons. Image: planets (electrons) orbiting the sun (protons and neutrons in a nucleus).
The classic/early model of this type is that of Niels Bohr, although many variations followed, often attempting to explain the observed magnetic moment by imagining a type of orbiting and spinning particle.45678
Experimental evidence indicated atomic orbits were stable. However, none of the early atomic models could explain why an orbiting particle would not radiate energy, thus losing the energy required to maintain orbit, resulting in a quick “crash” into the nucleus. Nor could they make the observed angular momentum match the observed magnetic moment by employing any classical physics model.
The GUTCP orbitsphere concept, a bubble of superimposed great circle currents symmetrically surrounding the nucleus that obey Newton’s Laws and Maxwell’s Equations, is novel in the scientific literature.
It is notable that one children’s book about atoms portrays an orbiting bound electron of an atom as having a “bubble” like structure as seen in Figure 4-2:
Figure 4-2: Children’s Atomic Model. An unintended deviation from SQM “probability” orthodoxy, published in a children’s book on atoms. This model clearly shares some orbitsphere characteristics.9
Given the physical orbitsphere model of the electron, the algebraic equations above have a set of allowed simultaneous solutions which result in quantized radii and velocity values. As noted, the single equation, Eq. 4-1, used to determine the velocity and radius of a satellite has a continuum of solutions. However, once the second fundamental equation is required, Eq. 4-3, there is only one specific “quantized” value of velocity and radii which is simultaneously a solution to both equations.
The GUTCP Hydrogen Model
Let’s consider the application of the general GUTCP model of atoms developed above to atomic hydrogen.
All that is required is a mathematical expression for the “central force” of Eq. 4-1 and carefully measured physical constants. Given the central force for hydrogen is the attraction between an electron and a proton, the classic description of this force is the very old Coulomb equation (1785), clearly consistent with all data and hence, “validated:”
where e is the charge on an electron/proton, epsilon0 is the permittivity of free space, and Z is the number of protons.
For hydrogen, Z=1. Combining Eq. 4-1 and Eq. 4-4 results in:
where me is electron mass. This equation has two unknowns, r (radius) and v (velocity).
To solve it, a second independent equation is required and this is simply the constant value of angular momentum, Eq. 4-3.
Organize Eq. 4-3 to express v as a function of r:
Next, replace v in Eq. 4-5 and solve for r:
No supercomputer is needed to solve this simple algebraic equation. Just combine the equation with a short list of constant values shown below in Table 4-1 and solve in a few seconds.
Solving Eq. 4-7 for the radius we that find r = 5.2917 x 10-11m. That is, the predicted GUTCP radius equals the famous Bohr radius, a0, the accepted value for the radius of hydrogen.
OK, the GUTCP passes the atomic size test, but how does one determine energy levels for comparison with spectroscopic data?
To solve for energy, classic pre-1872 physics is employed for an object in steady orbit: like the orbitsphere using STANDARD Maxwell/Newton equation analysis to obtain the binding energy (EB) which is equal to the kinetic energy, and for an electron is the ionization energy:
Predicted Energy: -13.6 eV.
Measured energy: -13.6 eV.
Also note that Z can be any value corresponding to the number of protons in a one-electron ion. For example, Eq. 4-8 predicts the binding energy/ionization energy of the one electron in hydrogen (Z=1), one electron in He+ (Z=2), the one electron in Li++ (Z=3) etc.
And further note, the theory is predictive. There are no “variable parameters.” It agrees with the data, or it doesn’t. If it fails to meet measured values, no dodges are employed, and it fails.
So, this equation is predictive for all atoms/ions with one electron.
A simple model that employs physics already demonstrated to be valid, and which matches multiple experimental data points precisely, retains validity. That is, any science model that predicts quantitatively the outcome of measurement is valid. A model only loses validity when it disagrees with actual measurement.
It is NOT the other way around. It seems popular in contemporary physics to question data that doesn’t match models. What??
As shown in Table 4-2, the GUTCP model, based on tested and validated classic physics equations, and well-measured physical parameters only, survives the one-electron system test!
The reader should note that the Source Text includes a relativistic correction term to the ionization energy calculation that is beyond the scope of this monograph. The fully developed GUTCP equation with the correction term calculates all one-electron atoms and ions to values well within the experimental error bars of experimental values.
Outcome
The GUTCP model passes Test 1: it agrees with every observation for hydrogen in the ground state, spectra, and magnetic moment*.
*Note to the Reader: The detailed description of the currents on an orbitsphere surface that create the magnetic moment is not addressed in this monograph. In the Source Text, the arrangement of great circle currents on the orbitsphere surface is provided. These currents are organized such that in sum all orbitspheres have the correct magnetic moment and the correct g-factor. Dr. Mills maintains the arrangement is unique, as no other could yield both the measured magnetic moment and the proper g-factor. Since the narrative around this issue is very, very involved, it is not included in this monograph. The key point is that the proposed arrangement of great circles precisely yields the known magnetic moment and g-factor of an electron. There is no equivalent in SQM. Magnetic moment and g-factor are just there. Moreover, the argument is entirely based on standard classic (Maxwellian) physics in which magnetic moments arise from current. The reader can either: A) trust this author, or B) wrestle with the current configuration provided in the Source Text. For the remainder of this monograph the author assumes you have done one or the other, thus further commentary on the details of the orbitsphere current pattern giving rise to the magnetic moment is not provided. In sum, the GUTCP model that the current pattern creates the measured magnetic moment, per classical physics, passes all the requirements of a valid physics theory: it is based entirely on classical physics, and agrees precisely, with no variable parameters or curve fitting, with observation.
The predicted energy level of ground state hydrogen is -13.6 eV, and that precisely matches the known ionization energy. Moreover, the same simple classic physics formula precisely predicts the measured ionization energy of every known one-electron atomic system, per Table 4-2.
This finding alone establishes the GUTCP as a powerful quantum model: simple, 3-dimensional, consistent with classical physics in every regard, no variable parameters, and predictions that match measured values for all one-electron systems.
Some may note some connection between the GUTCP model and the old (1913) Bohr model (Figure 4-2), which was the preferred hydrogen model for more than a decade, of the atom.4
Indeed, both are based on classical physics equations only and envision electrons in quantized orbits of definite radius. Hence, there is some connection between the models; however, the GUTCP model, particularly the orbitsphere extended particle geometry, overcomes all the objections to the Bohr model that led to its rejection.
This is significant, because it was the severe limitations of the Bohr model that led to its replacement by the Schrodinger model.
Figure 4-3: Bohr Model of Hydrogen. Bohr planetary model in which particle structured electrons are found in stable orbits of precise radii around the dense positive charge nucleus. In the Bohr model it is simply assumed the electrons do not lose energy due to acceleration-induced radiation. There is also no explanation for the magnetic behavior of the electron. The ground state of hydrogen radius is computed to be the Bohr radius based on classical mechanics equations virtually identical to those used in the GUTCP.
The Bohr Model
Below, a brief digression is needed to review some quantum theory history to show that the GUTCP is a continuation of efforts, after a long hiatus, to explain quantum observations by employing classical physics.
The Bohr model and some subsequent variations were on the classical physics track Ref. 4 & Ref. 9).1011
The intent in all cases was to explain quantum observations employing classical physics. Unfortunately, these efforts were preempted, based on some obvious flaws, by the Schrodinger model, leading physics to jump the tracks and the shark. This author considers SQM to be a pernicious model responsible for a 100-year vacation from reality. The author is in good company, as Einstein thought so too:
“This theory [quantum theory] reminds me a little of the system of delusions of an exceedingly intelligent paranoiac, concocted of incoherent elements of thoughts.”
The GUTCP is intended to return quantum physics to the original classical physical laws track.
The problems with Bohr model all extend from the “planetary” assumption aspect, with the electron postulated to be a small object that circles the nucleus, much like the planets of the solar system circle the sun.
The planetary model inherently creates problems with matching experimental data. For example, it is not possible to explain why the electrons in particular quantized orbits are stable.
A point electron moving in a circular orbit is accelerating by definition, as its direction of motion is constantly changing. Experimental observation shows that accelerated point charges (such as the Bohr model bound electron) always emit radiative energy.
This means that the Bohr model’s point charge electrons in orbit should lose energy by radiation and subsequently crash into the nucleus.
And yet experimental observation shows that certain (magic?) electron orbits that are stable. Why? It was a question that the Bohr model swept under the rug by simply positing stable planetary electron orbits, rather than explaining from first principles why certain orbits could be stable.
A major impetus for the development of the Schrodinger model was the need to develop a non-radiative model.
As discussed later, the full implications of the Schrodinger model for the non-radiation of bound electrons were not immediately understood. Gradually, it became clear that an assumption based on rejection of all classical physics was required to explain non-radiation of bound electrons in the SQM model. Ironically, the Schrodinger equation was designed to create a model more consistent with classical physics (explaining non-radiation), but in fact created one completely inconsistent with all of classical physics.
In contrast to the Bohr model, and other physical electron models from nearly a century ago, the GUTCP model of the bound electron overcomes the radiation problem by modeling the electron as an extended particle: a distribution of superconducting great circle current loops that forms a bubble shape when bound to an atomic nucleus. Dr. Mills has shown that extended distributions of charge may accelerate without radiating, thus solving one of the key problems with the Bohr model.
Interestingly, other scientists such as George Goedecke also used classical physics to show extended distributions of charge, in particular loops of charge like the “great circles” of the orbitsphere (Figure 4-1), can turn at constant angular velocity without radiating.12 However, Dr. Mills is the only scientist to incorporate this finding into a model of the bound electron.
There are also experimental demonstrations that superconductor loops do not radiate, hence do not lose energy and maintain constant angular momentum indefinitely, a requirement of the GUTCP model (more on this later).
More Bohr Model Failures
There are other classical physics failures to the Bohr model. One regards building a multi-electron system. Indeed, despite years of effort, no satisfactory classical explanation for screening of the positive nuclear field by a planetary object was devised. And yet, screening is required to reduce the net field acting on “outer electrons” in atoms with more than one electron. Computations of expected energy levels for multi-electron atoms did not match measured values.
In contrast, the GUTCP’s proposed orbitsphere perfectly explains symmetric screening by inner electrons of the positive fields created by protons in the nucleus, thus reducing the net force on the outer electron. And the GUTCP model is entirely classical physics, leading to near-perfect predictions of very well verified spectroscopic data of all multi-electron, net zero or positive charged, atomic/ionic species.
Another objection to the Bohr model is the failure to provide a classical model that quantitatively explained the observed magnetic behavior of atoms. The arrangement of the great loops of current on the GUTCP electron orbitsphere surface perfectly explain the observed magnetic behavior of bound electrons, as well as yielding the correct “g-factor” (ratio of angular momentum to magnetic moment) on the basis of a purely classical physics model.
In the final analysis, as detailed later, only the GUTCP model predicts the spectroscopy observed for all atomic species without any violation of classical physics.
Is the GUTCP really the heir to the long history of efforts to use classic physics to explain quantum phenomenon? A consistent misrepresentation of the GUTCP is that it introduces new physics, hence is neither classical nor SQM-like.13 But, as described above, all computations based on the GUTCP only use classical physics, and classical physics forces and equations.
The only argument that has any merit in questioning the authenticity of the “classical only” claim is that the inclusion of h-bar, the standard measure of degree of angular momentum quantization, implies importation of a quantum, non-classical, notion.
However, this is not a deviation from classical physics, because incorporating measured properties of objects, such as measured mass, has always been a feature of classical physics. The GUTCP simply incorporates another measured property of electrons, constant angular momentum of h-bar, a value and property which is extremely well verified by experiments.
In sum, the GUTCP is the logical evolution to the Bohr model and provides a flawless joining of macro-scale classical physics and the quantum realm.
In the mind of this author, if the GUTCP and SQM were proposed at the same moment a century ago, the former would have been hailed as the new standard, and SQM would have become a forgotten historical aberration. Unfortunately, this did not happen; hence, it is an uphill battle to dethrone the SQM quantum king.
In later sections, it will be shown that the classical physics model GUTCP accurately predicts all measured phenomena for all atoms and ions, and it will be shown SQM does not. For example (more on this later), GUTCP precisely predicts all atomic ionization energies.
After demonstrating the agreement with accepted atomic forms, the controversial component of the theory will be examined in later chapters. That is, the GUTCP is extrapolated, using the same equations as above, to lead to an unorthodox prediction: there exists a form of matter not generally accepted, Hydrinos.
Hydrinos are states, plural, in which the orbitsphere electron of hydrogen, a physical bubble shaped object that surrounds the nucleus, is closer to the proton, and consequently at a lower energy, than previously observed or believed possible.
A set of Hydrino states, 136 to be exact, in which the hydrogen orbitsphere takes a series of radii less than the Bohr radius, are predicted to exist. It is postulated these Hydrinos are the actual identity of dark matter and that the formation of Hydrinos in the corona of stars accounts for the measured greater than 1-million-degree temperature of the sun’s corona.
This prediction, and the remarkable match to experimental observations, is considered in detail in the second half of this book.
As you, the reader, continues, ask yourself this question: which side of the Looking Glass is SQM on, and which side GUTCP?
The SQM Hydrogen Model
Let’s next briefly consider the SQM/Schrodinger model of hydrogen to provide a contrast with the GUTCP model. Even engaging in this exercise is forbidden in most of the physics community. Most regard SQM as “proven” and sacred; herein, apostasy is practiced simply by treating SQM as just another theory.
Yet, it is just another theory!
The SQM model is entirely based on non-classical physics. Really? Yes, it assumes electrons are infinitely small objects that do not obey Newtonian physics.
For example, the solution to Schrodinger’s equation for hydrogen produces a “wave function,” a function that yields a scalar value for every point in space. From this wave function a probability distribution in space is generated. Probability of what? Probability that the electron, for a one-electron system, will be found at a given spatial coordinate.
In SQM it is understood the electron is at one point in space at one moment and in another the next moment. How long is a moment? There is no velocity. There is no requirement that the electron moves to an adjacent position; it is not even, relative to other locations, “likely.”
It is just as likely that the electron jumps to the other side of the nucleus, or to the center of the hydrogen nucleus. There is simply no trajectory, a complete abrogation of classical physics.
Another non-classical issue: exactly what is the electron that has this probability? Generally, this troubling issue is ignored in the SQM literature, but the mathematics of this theory requires (more later) the electron to be is an infinitely small particle, implying infinite mass and charge density, also non-classical concepts.14
Another non-classical aspect of SQM regards the treatment of particle energy. Overall, the ground state electron in the SQM model of hydrogen has a constant and negative value (bound), give or take a very small “uncertainty.” This energy is divided into kinetic and potential components, with the division being a function of the immediate position of the particle. Far from the nucleus the potential energy is near zero, hence, to make the total energy constant, the kinetic energy must be negative. There is no meaning to negative kinetic energy in classical physics.
Another non-classical outcome of SQM is that for hydrogen the most likely location of the electron is at the origin, that is, in the nucleus. At this location, so close to/overlapping the proton, the electron, classically, has near infinite negative net energy. In classical physics this would mean the electron would be trapped in the nucleus. In SQM this conundrum is ignored.
Another gap in the SQM model is the non-model for the magnetic moment of electrons. It is experimentally well known that when the magnetic moments of the bound electrons in atoms are aligned, there is a net magnetism. Yet, no physical or even mathematical model is provided for this in SQM. The magnetic moment is just there.
This is not classical physics (i.e. Faraday, Ampere, and Maxwell) because in classical physics a current is required to produce a magnetic field. In the SQM model there is no current because there is no trajectory. (Contrast: the children’s model of the electron showing current moving around the surface of a sphere, Figure 4-2, provides a physical basis for a magnetic moment!)
The aspiring young scientist is likely to imagine the SQM term “spin” means some sort of motion like that illustrated. But, in the actual SQM theory nothing is physically spinning.
As a final note: for single electron atoms and ions, it is true that many theories have similar predictions for energy, electron radius, and observed spectra. However, those theories do not explain many observations regarding single electron systems that are thoroughly explained by the GUTCP, such as the origin of the magnetic moment, the constant value of angular momentum for electrons, the value of the g-factor that relates angular momentum to magnetic moment, or even why electrons in orbit do not radiate.
Still, the quantum theory does succeed to some extent to explain aspects of one-electron systems. In sum, there is some overlap in the predictions of the GUTCP and the SQM model; hence, if only one-electron systems are considered, it is possible to argue, if one bangs the table hard enough, there is no winner.
This leads to the next section: atoms with more than one electron. At this next level of complexity the GUTCP emerges as the undeniable winner!
The Helium Atom
The primary finding from the application of the GUTCP to the helium atom: it produces quantitative predictions which precisely match spectroscopic observation and does so with no adjustable parameters.
In contrast, SQM makes no predictions regarding helium. The agreement with data from SQM comes from complex curve fitting routines, designed to force SQM to match observation, and always involves at least two adjustable parameters.
To set the stage for the lengthy discussion of this point, it is valuable first to consider the SQM model of the energy levels of ground state helium, as shown in Figure 4-4 below.
The SQM Helium Model
There are a host of major difficulties with all the SQM models of helium:
The solved model equations are always approximations of the true Schrodinger equation. For example, the true equation is in six dimensions, and all the solved models are in three.
Even these simplified approximate models are based on curve fitting for a single parameter, energy. In essence, at least two parameters are adjusted until the energy values of the models match the values obtained with spectroscopy.
It is clear that the energy values chosen for the fit are incorrect! There is no Pauli Exclusion Principle (PEP), and in fact the two electrons in helium have distinctly different energies, yet in all the models only one energy is employed!
There is no magnetic force term in any model.
There are at least two infinities in the models which are finessed in mathematically absurd fashions.
All of these objections and more are given amplified critiques below. Are there serious scientific arguments that support the SQM model? No. Yet, after decades of exclusive control over the pedagogical narrative, and 99.99% control of the quantum component of the scientific literature, it is clear “everybody knows” that SQM is correct. As pointed out earlier, “everybody knows” is not a scientific argument.
Energy
The energy levels at -24.59 eV represents the standard assignment of the ground state energy levels of both of the electrons of a helium atom based on spectroscopy, and the PEP.
The former shows it requires 24.59 eV to ionize one electron in helium, and that much energy is released, as measured experimentally, when the He+ ion recaptures that electron.
The latter, the PEP, indicates if one ground state energy level of helium is known, the other must be the same (Figure 4-4). This universally applied RULE is not based on the Schrodinger equation or any other “first principle.” (Notably, the PEP is just one of many “rules” in spectroscopy. Most focus on “allowed” vs. “forbidden” transitions.)
The PEP was introduced as a purported means to permit matching between models and experimental data, but below this is shown to be absurd. In any case, the origin of the rather arbitrary PEP, which allows two electrons to have all the same “features,” including energy, and probability distribution, except for spin orientation, is a long story. For this monograph we simply show that the PEP, whatever its provenance, is completely inconsistent with spectroscopic data.
Another angle to consider regarding the PEP is the mathematical requirement: the “exclusion principle” of SQM requires an extra quantum number.
According to the accepted mathematical multi-electron model, no two bound electrons can have identical quantum numbers. Yet, according to the PEP, before the addition of the new quantum number, the two electrons in the ground state of helium did have identical quantum numbers.
As the theory developed in the early twentieth century, this was overcome with the addition of a new quantum number, the spin quantum number, with two possible values. This new quantum number was associated with the physical orientation of the magnetic moment of a bound electron in space.
Hence, there is no mathematical violation of the “no identical quantum” number rule as long as the spin numbers/magnetic-moment-direction are different. Assigning a plus and a minus spin means two electrons can have the same expectation value for energy, radius, etc. in the helium ground state, but differ only in the direction, and value, of the assigned magnetic quantum number.
Hence, any particular orbital in SQM can have two electrons. For example, the two electrons in helium according to SQM are identical in all fashions, except for opposite, and cancelling, magnetic moments, magnetic quantum numbers of +1/2 and -1/2, corresponding to magnetic moments pointed in opposite directions.
Figure 4-4: Restricted Electron Populations. According to the Pauli Exclusion Principle, no two electrons have the same quantum numbers. The two electrons in ground state helium have all the same quantum numbers except for the spin quantum number, +1/2 and -1/2. One has a PLUS spin and the other a MINUS spin. For this reason, these electrons are identical in all respects, including expectation value of energy, except for the direction of spin. The opposite alignment of spins mean the magnetic fields cancel.
Another topic under the umbrella of SQM helium energy states are “excited” states. In SQM, an electron in the helium atom ground state can be excited into a higher energy state by absorbing a photon. If the absorbed energy is sufficient, the electron leaves the atom altogether in a process called ionization. The excited states are very short lived and fall in energy with release of the(the same?) photon that created the excited state. These released photons are characterized for wavelength and energy using spectroscopy. It is this spectroscopic information that provides evidence of the allowed quantized energy levels in helium and other atoms.
The processes of excitation, de-excitation, and ionization are part of the discussion of the failures of the SQM helium model, as discussed below. There are other related questions which are addressed in Chapter 5.
The process of forming an excited state requires absorption of a photon. In SQM this leads to the question: where did the photon go (more on this in Chapter 6)? Another major question: why is it that these excited states are not stable, with a lifetime of the order of only 10-7 seconds?
In Figure 4-5 below the standard physics model (SQM) of the ionization of helium is presented schematically. As shown, it is a two-stage process. In the left column there are three groups of states shown: i) the two electrons in their ground state are shown (-24.59 eV), ii) a schematic, conceptually correct, set of the excited state (>-5eV) energy levels, and iii) and the energy level of the one electron that is present after ionization (-54.4 eV). The energy levels of the excited states are not precise in the diagram, as there are too many excited states above -4eV, closely spaced in energy, for ready representation. In any event, the details of the energy levels of the excited states are not germane to the argument.
Figure 4-5: The Conundrum of Helium Ionization Energy. The energy levels occupied by the electrons of helium in the ground state and after ionization energy are shown with + sign. All energy levels observed spectroscopically are shown in red. Where does the energy go, ~30 eV (central energy level pictograph), when one electron falls to -54.4eV from the initial double occupancy state at -24.59 eV?
The central energy level pictograph in the figure, “Excited State,” shows a possible first step in ionization. This is only a possible first step for a multi-step ionization. Experimental data clearly shows ionization from the ground state can occur in a single step, two steps, three steps, etc. The focus herein is on a two stage process in order to raise, in the simplest possible manner, some energy conservation issues.
The most significant take-away from the presumed two-step process being followed here is the energy history of the electron which is not excited.
According to the standard physics theory, when an electron in helium, a two-electron atom, is promoted to one of the excited states, or is directly ionized in a single step, the other electron , the “not excited” electron, falls in energy to -54.4 eV at precisely the same moment, as illustrated in Figure 4-5.
According to the Newtonian “law” of energy conservation, almost +30 eV should be released, as a photon, when the not-excited electron initially in the atomic ground state falls to its final energy level, an energy level, according to SQM, only available after ionization or excitation occurs.
Thus, in this column, one electron is shown in an excited state at about -4 eV, and the other electron is shown to be in the minimum He atom energy of -54.4 eV.
Finally, another photon is presumed to be absorbed, with just enough energy, about 4 eV, to promote the “excited” electron into the vacuum.
The electron at -54.4 eV does not change energy state according to the generally adopted standard model. Thus, in the column labelled “Ionized,” one electron is shown with 0 energy, while the other is still at -54.4 eV.
It is important to note that the only quantized energy levels shown in Figures 4-5 above and 4-6 below correspond to actual measured energy levels as determined by spectroscopy. In other words, the quantized energy states shown can be directly correlated with spectroscopic data.
In contrast, the “relaxation” model (discussed below) requires states that do not exist according to spectroscopy. Indeed, it is argued later that to save the PEP from failure due to inconsistency with energy conservation, that is to solve what herein is called the energy conservation conundrum, a process called relaxation must exist.
In turn, the relaxation model requires the postulated existence of energy levels for which there is no spectroscopic evidence.
In particular, later in this chapter it is shown that states at -39.5 eV, as well as other energy levels, must exist to conserve energy according to the SQM relaxation model of helium. This requirement of SQM theory is contrary to science, because to validate a theory experimental data must support it.
There is no data supporting a state at -39.5 eV.
To re-phrase: in order for any PEP consistent model to establish energy conservation, as described below, it requires the existence of quantized energy states for which there is no experimental evidence.
The logic, from the SQM community, is a form of circular/backwards science reasoning: "the states with no spectroscopic signal must exist because the theory is correct. The data is clearly seriously flawed!” Details on this later.
And yes, the only energy preserving SQM model of helium, the “relaxation model,” is scientifically untenable because no data can be found to support the existence of quantized energy states required to support energy conservation.
The reader may reach an understanding of the energy conservation conundrum based on consideration of two questions. First, if both electrons in helium in its ground state have the same energy value, and it is the value universally given as approximately -24.59 eV, where does the energy (~30 eV) go when one electron is either excited or ionized, and the other falls to the -54.4 eV state?
THINK! This is an energy conundrum because the answer is: SQM fails to close the energy balance/conservation of energy required in all physics.
This is illustrated in Figure 4-5 where the + signs indicate the energy levels occupied by the electrons at the end of each process.
And second, where does the energy come from to promote the electron back from -54.4 eV to -24.59 eV when the ionized helium recaptures an electron and releases, as per uncontested observation, a 24.59 eV photon?
Again, this is another look at the energy conundrum of the standard assignment of energy levels before and after excitation of the He atom. SQM, again, fails to close the energy balance/conservation of energy required in all physics.
The above are not trick questions. These are the energy values almost universally postulated to be the initial energy of the electrons before ionization (and after electron re-capture), and final energy levels of electrons after ionization.
Something to consider as you contemplate these conundrum riddles: there are those who will argue, disingenuously, that net energy change it is a function of “process.” No. This is a first law of thermodynamics question, for which only the end states matter. Process is irrelevant for energy change between any initial and final states.
Example of 1st Law Thermo: if a bowling ball is initially at the bottom of a 100-foot hill, and after some process is at the top, the potential energy change of the ball is the same: mbb X g X 100 ft, independent of process. (mbb is the mass of the bowling ball, g is the gravitational acceleration constant at the earth’s surface, and 100 ft is the change of height, and g is the gravitational constant at earth’s surface.)
This value is not a matter of “how.” It is the same if the ball is:
Lifted by a helicopter.
Taken to the airport, flown around the world and then dropped with a parachute.
Carried up on the back of a bicycle.
Pulled up by a goat.
In all cases the change in potential energy is the same. The energy change is not process related. And if your eyes are averted during the process, you will not know the how the ball was moved or its path, but the change of potential energy will be absolutely clear.
Similarly, if the two electrons in helium are initially at -24.59 eV, one is ionized and the other drops to -54.4 eV, any model must provide a full accounting of energy, and the energy accounting component of the model must be process independent. It must be independent of how because energy is a state property. Energy is not lost, no matter the process.
To understand energy conservation, think like an accountant with energy as the currency.
Figure 4-6 - Energy Level Diagram of Helium in Ground and Excited States. H. Bethe reports that both electrons are initially in the 1 S state, -24.47, yet the value of the first ionization energy of helium is now accepted to be -24.59. This small range of reported experimental values suggests a small disagreement between the GUTCP prediction and the accepted measured value may simply reflect some “wiggle” in the value of the latter. (Ref. 15, Fig. 27).15
The discussion of energy levels in helium is intended to be rational and simple, and probably is to the “uninitiated,” however, it is emotionally disconcerting for those formally trained in physics and chemistry, because the net outcome is the rejection of the PEP, a central paradigm of all the text-book descriptions of helium, in fact, of all multi-electron atoms and molecules.
For this reason, the next few paragraphs are included, although they essentially repeat the paragraphs above.
In this second version, the energy conservation argument is written in the language of chemical reaction, just to present it in a more formal manner. This somewhat redundant narrative section is included as a means of reinforcing, and further “socializing,” the narrative that falls out of the GUTCP description of helium, as proposed by this author:
There is no PEP. It is wrong. No two electrons in an atom have the same energy and size.
If both electrons in the ground state are at -24.59 eV (Standard Model) as generally understood, as shown in Figure 4-6, composed by Nobel Prize Winner Hans Bethe, then to remove one electron (ionize) requires an input energy of 24.59 eV (Ref. 4-15).
In fact, this is the universally observed first ionization energy of helium. However, as it has been experimentally demonstrated countless times, the remaining electron requires an additional 54.4 eV to be ionized. For this reason, as per Figure 4-5, after ionization, or after excitation without ionization, the second electron is always presumed to be at an energy of -54.4 eV below the vacuum level.
Why is the above energy level description a conundrum? Here, in the language of reaction chemistry, is the net energy of the process to create He+ and a free electron, assuming the model of SQM, that is the one step ionization process (left most column of Figure 4-5, then ionization per the right most column):
Step 1:
Step 2:
The * term represents the energy change of the “un-ionized” electron, e2, in “He+ (initial state),” that is at -24.59 eV, the generally presumed starting energy of both electrons in helium. Per standard model this electron, e2, upon removal via ionization of e1, immediately drops to a lower energy, -54.4 eV.
Energy must be released by this process for energy conservation!
Indeed, the final stable state of the “un-ionized” electron, e2, is always presumed in the literature, based on spectroscopy, to be -54.4 eV. Hence, the energy released is the final state (-54.4 eV) minus the energy of the starting point (-24.59 eV), or 29.9 eV.
In sum, the process of helium ionization in this SQM model RELEASES net energy. The energy, 5.3 eV, is not trivial; it is more than 4 times the energy of oxidizing hydrogen.
Crazy.
There is no experimental evidence of any ionization process that RELEASES net energy. The conundrum gets worse if the remaining electron is removed, per this model:
Step 3:
That is, per the model, 54.4 eV are required to remove the one electron from He+ creating a zero energy free electron, and a He++ nucleus. Note, the Step 3 ionization energy, -54.4 eV, agrees with data.
What happens to the He++? It is very unstable, and ‘wants’ to grab two electrons, in order to become, once again, a neutral helium atom. Hence, it is repeatedly observed that He++ will spontaneously absorb two free, zero energy, electrons, releasing 79.1 eV. This can be written:
Step 4:
This leads to the following net energy equation for a round trip from He0 to He0:
Total energy: (step 1 + step 2) + step 3 + step 4 = (5.4 eV) - 54.4 eV + 79.1 eV = +30.1 eV (energy released)
The round-trip process of full ionization (two electrons), followed by re-capture of two electrons, according to this model releases an enormous amount of energy per helium atom, more than 20 times the amount created by burning one hydrogen molecule. Clearly, according to this model the world can solve all its energy problems by sequentially fully ionizing helium and then allowing the ionized helium to recapture electrons.
Great Model? - NOT!
SQM Helium Relaxation Model
It is possible to contrive an energy scheme that does not have the energy conundrum described above, and simultaneously retains the PEP.
This model, a type of model based on the concept of relaxation, is illustrated in Figure 4-7 below, postulates the two electrons of helium in the ground state are at -39.55 eV, such that in total they have -79.1 eV of energy. All processes from this state are complex, involving taking energy from multiple “accounts” and adding them together to make a single “purchase.”
Ionization, for example, requires instantaneously taking the energy from an absorbed -24.59 eV photon, and adding to that account the energy that is freed up when one of the electrons initially at -39.5 eV “relaxes” to -54.4 eV, a total of ~15 eV.
Energy from these two accounts, absorbed photon and relaxation, are added together, instantly, to “purchase” the freedom of the other electron that was originally at -39.5 eV, that is 24.59 eV + 15 eV ~ 39.5 eV.
Figure 4-7: Relaxation Model Helium Quantized States. Note, the solid lines represent the measured energy levels from the spectra of helium. The dashed “states” are required for the relaxation model, but do not correspond to any measurement. For example, the relaxation model requires both electrons in the ground state to be at -39.5 eV. There is no light emission even close to this energy value in the observed helium spectra.
A similar multiple account process is required to excite one electron. In the excitation process a photon with ca. 20 eV, not enough to ionize, is absorbed by one electron at the postulated/model required (no spectroscopic evidence!) -39.5eV. (Note the value 20 eV closely corresponds to a measured energy in the helium atom spectra, Figure 4-6.) Simultaneously, the other electron at -39.5 eV falls to a lower state, yet somewhat higher than -54.4 eV, as illustrated in the Excited State Column of Figure 4-7. That is, it falls to an energy level (dashed lines in the figure) which is assumed to exist.
Assumed? No feature in the helium spectra even remotely corresponds to this energy level. The energy level the excited electron finally occupies also is assumed to exist. Indeed, the additional measured energy required to ionize the excited electron is about 4.5 eV, but this energy also involves two accounts: energy of the absorbed photon, and the final step down to -54.4 eV of the other electron.
Clearly, as shown in the Ionized column of Figure 4-7, the energy level of this excited state must be more than 4.5 eV, the measured value, below the vacuum level, or there would be no place for the final step “relaxation energy” of the other electron to go.
Perhaps this process is too hyper-complex, with processes postulated to occur for which there is no experimental evidence, to be real; perhaps it sounds more like a bunch of gibberish than a serious model?
The above relaxation model of helium energy levels is not found in any peer-reviewed publication! There is no published alternative to the model of allowed energy states proposed by Bethe (Figure 4-6), who posits that the stable states of helium precisely correspond to features in the helium spectra.
However, it must be noted that the relaxation concept is employed in quantum models all the time, although not for helium. In particular, there are many molecular orbital models that depend on this concept of relaxation. Relaxation: one electron in an atom or molecule increases its energy both via the absorption of a photon, PLUS an energy kick from energy provided as one or more of the remaining electrons relax to lower energy levels.
Is relaxation a part of the Schrödinger model? Is there any theoretical basis? Is it the solution to some equation?
No, No, and No.
Relaxation is an ad hoc postulate that allows the modeler to satisfy both energy conservation and the PEP. It is also very clearly metaphysics, as defined earlier.
Critique of SQM Helium
As noted in classic books co-authored by three different physics Nobel Prize winners, the SQM wave equation for helium, the second simplest atom, is unsolvable.
To quote Bethe (Nobel laurate) and Salpeter (Ref. 4-15, Section 25):
“The differential equation….for the two electron system is not separable…(hence)…the solutions for the eigenfunctions and energy eigenvalues cannot be expressed in closed analytical forms. We shall have to use various approximation methods…”
Or as stated by Pauling (Nobel Laurate) and Wilson (Ref. 4-16, Chapter 6):
“Thus even the simplest many-electron systems, the helium atom and the hydrogen molecule lead to wave equations that have not been rigorously solved. In order to permit the discussion of these systems….various methods of approximate solution of the wave equation have been devised…”16
And finally, a third text by a Nobel Prize winning physicist, Landau (Ref. 4-17, Section 69):
“Schrodinger’s equation for atoms containing more than one electron cannot be directly solved in practice even by numerical methods. Approximate methods of calculating the energies of the wave function of the stationary states of the atoms are therefore important.”17
As discussed in detail elsewhere these “approximations” are better described as alternative quantum models. That is, they use the same words as in true SQM, words such as “wave function” and “probability,” but the mathematics are completely different.1819
A second issue is the fundamental objective of the approximate equations used in SQM to model helium. These approximations are not intended to predict the wave functions/probability distributions of the electrons in helium, but rather to adjust the theoretical (i.e. unobserved) wave function until the energy derived from the mathematically contrived wave function matches the spectroscopically measured values.
In other words, the intent is to curve fit the solution to match measured spectroscopic energy level values.
In all of these approximate models at least two variational parameters are optimized for each electron to make the curve fit energy match the measured energy. Moreover, as discussed elsewhere, there are a dizzying number of approximation methods, and the complexity of the methods appears to escalate as the available computing power to optimize solutions increases.
It is a long and tedious process to review all of this complex literature here, thus the reader is referred to published detailed analysis provide elsewhere (Ref. 4-18 & Ref. 4-19).
Rabbit hole.
A third issue for the SQM model of multi-electron systems is the “active disappearance” of infinities. In the following discussion of the electron-electron interaction component of the energy computation for a multi-electron system, two examples of this active disappearance of infinities are presented, as well as a number of other issues connected with computing electron-electron interaction energy.
For two electron systems the mathematics for determining the wave function, the Hamiltonian (H), is written in non-operator form:
where “p” is the momentum, “Z” is the nuclear charge, the “r” are positions of electrons 1 and 2, and “m” is the reduced mass. The H, Hamiltonian, operating on the wave function yields the electron energies.
The non-operator Hamiltonian for two electrons, above, is very similar to that of one-electron system, except for the last term. In brief, above is the Hamiltonian which is best understood as a total energy equation for the two electrons. The first term (p12/2m) represents the operator which yields the kinetic energy (always positive) of one electron, and the second term the operator yielding the kinetic energy of the second electron. The third term (Ze2/r1) is negative because it is the binding energy operator which returns the energy due to the interaction of electron 1 with the protons in the nucleus (e.g., Z=2 for helium). The fourth term is the same as the third except it is for the second electron.
The fifth and last term is special. It is the last term which represents the operator for energy of interaction between the two electrons. It is not present in the one-electron system, as there is no second electron with which to interact. The form of this interaction term indicates the energy of interaction gets larger the closer the two electrons are.
This makes intuitive sense: two objects of the same charge repel each other, with a strength proportional to 1/r2. The closer the two objects, the smaller the value of r, the stronger the repulsion force.
Energy is the integral of force over any path, from infinity to the final position. As energy change is path independent, this integration process simply leads to an energy of repulsion proportional to 1/r1,2, where r1,2 is the final separation distance between the electrons.
This term is always positive because it is a repulsion. It takes energy to push against a repulsive force, hence positive energy is stored in the interaction. In a sense it is an “anti-bonding” force.
This term merits more detailed examination because it is in this term that all the pathology of multi-electron SQM, including clear infinities, is hidden.
And note: There is no magnetic interaction energy in the SQM model! The model is missing a major energy term, by design!
The equation below is the mathematical, quantitative recipe for determination of the TOTAL energy of electron-electron interaction from the wave function (psi) derived from the expression for the Hamiltonian:
Specifically, the equation expresses the process of computing the total energy of electron-electron interaction.
How? First, the interaction energy at any particular value of r1 and r2, is determined by multiplying the energy operator determined energy:
by the probability that the two electrons are found at points r1 and r2:
Note the probability at any point in space is a positive value, and always in the range of 0 to 1. Also note the probabilities of all points in space sum to 1, because there is a perfect probability that the electrons are somewhere.
The sum of the interaction energies is determined by computing the above value for all possible r1 and r2 values. This is done by integration, a process roughly explained thus; first mathematically, place one electron at a point (r2), and then move the other electron to all points in space (r1). Naturally, at each point the value of the wave function/probability, psi, at that point must be re-computed.
Next, repeat the process but with a different r2. Hold r2 in the new spot and move r1 over all space again. Do this until r2 has occupied every point in space. The probability adjusted energy values obtained for all the r1 - r2 values are then summed/integrated to yield the total “probable energy.”
Lots and lots of computation, BIG computer needed.
Clearly, SQM mathematics can be daunting, no doubt about it, but the real issue is many irredeemable flaws, outlined below.
First Flaw
The unstated assumption in the math, based on the “location” parameter rx, is that the electron is located at a single point. One electron is located at r1 and the other at r2. The pathology here is the physical meaning: each electron is at a point in space, hence is a zero-dimensional object. (As noted before, there is some vague philosophical discussion in the standard quantum community about “particles riding waves,” etc. but as shown in this discussion of the Hamiltonian, where the equations meet the mathematical road, the electron must be a zero-dimensional object found somewhere.)
A zero-dimensional object has zero volume. But the electron has mass in SQM, and this leads to infinite density. Indeed, density = mass/volume, and as the electron has no volume, this ratio is infinity. Is the electron like a mini black hole? This is the first of two hidden infinities in the most basic SQM mathematics.
Second Flaw
A second hidden infinity is inherent in the denominator of the energy operator. Specifically, every time r2 is set, and then r1 is varied over all space, as per above description of the integration process, there will be an infinity.
That is, this process of varying the position of r1 will always include a spot where r1 = r2. Intuitively and mathematically, this leads to infinite energy of repulsion. Indeed, at the spot where r1 = r2 the denominator in the energy operator goes to zero, so the repulsive energy goes to infinity.
Moreover, the probability value, always positive and between 0 and 1, is not going to mitigate the infinity. Specifically, the product of probability, however small, and energy when r1 = r2 is always infinity. The sum of a single infinity, and many finite values, is always infinity.
Bingo: Inherent in the mathematics of SQM of multi-electron systems is infinite repulsive energy between electrons.
How does the SQM community “get over” this infinity problem? “Sleight of mathematics” is one means.
Old methods, based on replacing 1/(r1-r2) in the energy operator with some monstrous mathematical “equivalent” is one approach. These substitutions are clearly not correct. Indeed, if they were correct there would always be an infinity. The substitution is made in order to avoid the infinity, so it is designed to be incorrect.
That is, the error is never an error, it is a “deliberate.”
For example, Eyring et al. suggested the following equality, widely used, could be used and would lead to a finite value of the repulsive energy:20
Eyring’s proposed substitution leads to the above expression, one in which the equal sign is clearly wrong. Indeed, consider that r< is at the origin, that is r< equals zero, and r> is any point but the origin, hence has a non-zero value.
In this case, every term in the sum has a zero value, thus the sum equals zero. Not correct!
It is obvious that as r< and r> are not the same point, the actual value of ri,j, the length of the vector joining the points, is not zero. So, not only does the Eyring substitution not solve the two-electrons-are-at-the-same-point issue, but it also doesn’t give a proper value for the vector length of a line joining two distinct points.
Moreover, the possible counter argument that the origin point is special is mathematical nonsense. The value returned by any equation purporting to compute the distance between electrons must be independent of where the origin, or any other point, is placed. Further discussion of this infinity issue is found elsewhere (Ref. 4-19).
The community uses other methods to ignore the obvious infinity, particularly a throw-in theory called correlation.21
This concept means that the two electrons perform a dance in time such that they are never at the same point at the same time. The electron positions are “correlated.”
Oddly, this assumes a type of trajectory for each electron, an idea inconsistent with the fundamental probability notion of SQM. This is an arbitrary assumption. It is not part of Schrodinger’s equation, and it does not generally have a mathematical expression.
There are exceptions to this latter point in some approximate solution protocols. For example, in the SCF-Xa method an extra electron-electron repulsion force term, one for which there is no basis in experimental physics, is added to the electron-electron energy term to reduce the likelihood that the two electrons can overlap.22
The magnitude of this repulsion? Like so many features of standard quantum models of atoms, there is a variable parameter that determines repulsion force strength. This parameter is varied until the method yields the best fit to the experimental data.
Third Flaw
The Coulomb expression for electron-electron and electron-proton interactions are unaltered classical force laws. Newton’s Laws were abandoned, why not the Coulomb interaction as well? Why keep some classical laws and not others? Indeed, as noted above, in the SCF-Xa approximation method, the developers appear to ask the same question and reach the conclusion the classic Coulomb’s Law can be adjusted in order to obtain a better match with data. Why not?
Fourth Flaw
The expression for the electron-electron interaction energy contains no magnetic interaction term. And yet, it is experimentally known that each electron has a magnetic moment. How can the necessary interaction energy, attractive or repulsive, associated with two magnetic bodies be ignored?
Other Flaws
In addition to the above list of irredeemable flaws listed for the electron-electron interaction term there are a host of other major logic leaps employed to create computationally tractable approximations from the true quantum theory. Among the other issues: in the full, by all accounts mathematically unsolvable, multi-electron version of SQM, each time an electron is added to the system, three new orthogonal dimensions are required.
This is a mathematical requirement, basically impossible to explain or illustrate. Rather, the formality of this 3X multiple dimensions is described. Specifically, the required 3X, where X is the number of electrons, multi-dimensional requirement of the unadulterated Schrodinger model is best expressed, mathematically, employing the Slater Determinant. It is a very complex mathematical expression that this author has previously attempted to explain in physical terms. Rather than reproduce the argument, the reader is directed elsewhere (Ref. 4-18).
It is notable that one outcome of the “3X the number of electron dimensions” argument is that for all electrons to be indistinguishable, per the rules of SQM, there can only be ONE wave equation for all the electrons in a system. And note, this is contradicted by other accepted notions.
Indeed, if the system is an atom which has ten electrons that are indistinguishable, it is not possible to say two are in a particular orbital and the other eight are in different particular orbitals. The electrons would, in such a physical world, be distinguishable. Hence, the “each electron is in a specific orbital” argument, and the PEP, are incompatible with the true Schrodinger model of multi-electron systems.
In particular, the PEP is inconsistent even in a three-electron system. Two of the electrons are paired, according to PEP, and the other is necessarily different/distinguishable. This is clearly not in harmony with the rule of indistinguishable.
In the unmodified Schrodinger model the helium solution requires six dimensions, lithium nine, etc. Where are these dimensions? Where are the electrons?
Notably, the solved approximate models for multi-electron systems all have three dimensions only. Can a model be labelled as approximate if it drops whole dimensions?
In the full multi-electron model, electrons are indistinguishable such that there is only one wave function for the two electrons of helium, the three electrons of lithium, etc.
However, in all the approximate methods there is one wave function for each electron. The electrons are very definitely distinguishable. Is this a legitimate approximation? Is the “unapproximated” true theory even remotely consistent with spectroscopy which clearly shows the electrons are in different, distinguishable, energy levels?
In sum, in addition to the energy conundrums of the SQM models of the energy states of the electron in helium there are a host of mathematical/physical issues, briefly reviewed above. These and other issues are reviewed elsewhere (Ref. 4-18 & Ref. 4-19).
A Summary Of The Issues
The wave equation for a two-electron system requires there be six orthogonal spatial dimensions. A three-electron system requires nine orthogonal dimensions, etc. Where are these dimensions? Where are the electrons? The approximate models are in three dimensions. Is a model that arbitrarily drops multiple dimensions really an approximation?
The wave function for a two-electron system consists of a scalar value at every point in six-dimensional space. The integrated sum of all these values is ONE (not two). What is the meaning of the scalar wave function value at each point? For a single electron, represented by a three-dimensional wave function, each scalar value is purportedly the probability that the electron is at that point. The overall, integrated probability is ONE, as it should be. Given the above description, what is the meaning of the scalar value for each point of six-dimensional space (two-electron system)? What is the meaning of the wave function? Is it the probability that both electrons are at that six-dimensional point? Where are those dimensions? Where is that point? Where are the electrons?
One can draw a three-dimensional probability map and label it an “s-orbital” or a “p-orbital,” etc. How does one draw the six-dimensional orbitals of helium, or nine-dimensional orbitals of lithium?
There are always ludicrous methods employed to “work around” infinities.
From what property of the electron wave function does a magnetic moment arise?
Finally, noted is the near-absurd complexity of actually solving any set of equations, no matter how approximated, to obtain values that can be compared to measured data. To solve the helium atom using any and all approximations requires an enormous computational effort (think: very large supercomputer) to optimize the values of at least two variable parameters (depending on which approximation is used) per electron. It is an exercise in curve fitting.
Not only is the SQM model of helium an exercise in over-the-top complex mathematical curve fitting, but there is also a fundamental issue regarding what experimental values are to be fit. Indeed, for helium atoms in the ground state, the present paradigm, used in the development of all the approximation models, is that both electrons are of the same energy, per the PEP.
This leads to a question: What is the energy of the two electrons that the fitted model should produce? Is it the measured first ionization energy? Is it the measured second ionization energy, which is more than twice the first ionization energy? Most models assume it is the first measured ionization energy. A few suggest, without any spectroscopic evidence, that it is an average of the two, per the relaxation model.
Note: All alkali earth metals are presumed to have an “outer shell” electron configuration similar to helium, that is, a pair of identical s-electrons. However, like helium, the second ionization energy for alkali earth metals is always approximately twice that of the first ionization energy. In other words, there is no spectroscopic evidence to support the PEP from any doubly filled outer s-electron shell. Again, the simplest explanation of the spectroscopic data for alkali metals is that there is no PEP! The two electrons in the outer orbit NEVER have the same energy or size.
The GUTCP Helium Energy Analysis
There are TWO GUTCP models for helium. One is the version found in the Source Text, herein “ST,” and the other is the Mod 1 GUTCP model, herein “Mod 1,” introduced by the author of this monograph in 2007 (Ref. 4-19).
The chief difference is that in the ST model the PEP is assumed, whereas in the Mod 1 version it is rejected. That is, in the ST model, after all radius and velocity computations are complete, the PEP is presumed and both electrons are assumed (forced!) to have the same radius and energy, that of the outer electron.
In contrast, in the Mod 1 model, it is presumed that the PEP is nuts, and thus the final radius and energy of each electron is what the uncontaminated and raw computations indicate.
Each electron has its own, unique radius, velocity, and energy. It is argued below that only the Mod 1 version has no energy conundrum. This is summarized in Table 4-3.
It is explained below that both the GUTCP ST and Mod 1 models of helium are superior to SQM in every respect. Neither has the weirdness of SQM:
There is no Correspondence Principle.
There is no uncertainty.
There are only three dimensions.
The magnetic field results from moving current.
Only classic physics equations and measured constants are required.
Everything can be solved exactly using simple algebra with no variable parameters.
However; it is further argued that the Mod 1 model is the superior GUTCP model as there is no complex intellectual wrestling required to bring it in alignment with all known data. Specifically, there is no energy conundrum and there is no PEP, whereas with the ST model the same energy conundrum outlined above for the SQM model exists.
The GUTCP ST Model
In this model the helium atom is built in stages. First, one electron is added to a two proton nucleus:
He++ -> He+
The radius, energy (-54.4 eV) and velocity of this electron are computed using a force balance and conservation of angular momentum (below). Next, the second electron is added:
He+ -> He0
And again the radius, energy (-24.59 eV), and velocity of the (second) electron are computed using a force balance and conservation of angular momentum (below).
But at this point, some complex arguments are employed explain the energy level assignments in the ST model. The reader is invited to visit the Source Text to follow the argument.
In substance, this results in the “re-organization” of the energy and radius and the declaration that both electrons of He0 have an energy of ~-24.59 eV, and also the same radius.
In net, Figure 4-5 applies to both SQM and the GUTCP ST models. Both the SQM model and the GUTCP ST model, as explained earlier in this chapter, have a massive energy conundrum.
The GUTCP Mod 1 Model
In Figure 4-8 below, the directly predicted Mod 1 model of energy levels in helium, described in mathematical detail below, is shown. There are very sharp differences with the ST model, as summarized in Table 4-3.
Figure 4-8: GUTCP Mod 1 Model of Helium Energy Levels. In contrast to the Standard Model of Helium Electron Levels (Figure 4-5) there is no PEP, thus the two electrons of helium are never at the same energy state. There is no energy conservation conundrum. The model is completely consistent with spectroscopically determined quantum levels in helium.
The Mod 1 model is the only model with no energy conundrum. For example, assume during excitation helium absorbs a photon, e.g. 20 eV. In this model all that happens is straightforward: the “outer” electron (-24.59 eV) moves into a higher energy state exactly that many eV above the ground state. There is no concomitant change in the energy level of the “inner” electron (-54.4 eV).
When the excited electron falls back to the ground state, a photon of exactly 20 eV is returned, such that energy IN equals energy OUT, without the need to assume a complex two body coordinated process/dance, as per the “relaxation” model.
There is also no need to require the existence of stable states between -24.59? eV and -54.4 eV (ca. Figure 4-7) for the inner electron to move in and out of, states for which there is no, absolutely zero, spectroscopic evidence.
Another example: when an ionized helium recaptures an electron, it goes to the ground state, -24.59 eV, which is exactly the energy of the photon released such that energy is conserved. That is the entire process. There is no complex accounting for energy via some relaxation process.
Also, unlike the SQM model, or the GUTCP ST model, there is no need to explain an energy conundrum. During the process of electron capture the inner electron does not change energy level. It starts and ends at -54.4 eV.
Accountants, be happy!
Mathematical Development of the Mod 1 Model
The GUTCP Mod 1 model is now developed in detail. This is the preferred model herein as it is the only model with no energy conundrum. The model uses the same two algebraic equations, force balance and momentum conservation, described for single atom systems. Unlike SQM, the totally predictive helium mathematics are simple enough to describe in detail below, and there is no need to explain the various hocus-pocus methods used to get around infinities, etc that SQM relies upon. Why not?
There is no hocus pocus.
There are no infinities because the electrons, orbitspheres of different dimensions, do not touch. This is the essence of a new GUTCP Mod 1 Exclusion Principle: like-charged particles never touch.
The only change in the mathematics relative to that used in the GUTCP hydrogen model is the increase in the Z value for the inner electron and the addition of a magnetic term to the central force in Eq. 4-1 for the physically larger “outer” electron.
Note, both electrons are orbitspheres (Figure 1) of different radii (see below development), one nested inside the other.
Inner Electron of Mod 1
The Mod 1 model of helium requires building the atom one electron at a time. The building starts with force and momentum balances for the inner electron (electron closest to nucleus).
The GUTCP model helium atom is built in stages to reflect the different central force each electron in ground state helium experiences. The same force balance employed earlier for single electron species is employed, and in fact the entire analysis looks identical to that done for one-electron species:
Where me is the mass of the electron, v is the velocity of all rings (unknown), and r is radius of the electron (unknown).
The “maths,” contrary to the arguments of the SQM community, just aren’t complicated, and contain no new physics!
For those who want to get technical, the equation for each ring of current loops that comprise the orbitsphere can be considered independently:
Eq. 4-12 can be summed over all the great circle rings, each having the same velocity and radius, and it leads to Eq. 4-13, where the sum of the masses of the rings is the mass of an electron, as per NIST website.
The only “central force” in the first equation for the first electron is the Coulomb attraction between charges of different polarity. The construction of the first equation of He+ is thus:
Where Z is the number of protons (two for helium), e is the charge on an electron/proton, m is the mass of an electron, and epsilon0 is the permittivity of free space.
There are two unknowns, v, the velocity of the rings, and r, the radius of the inner electron orbitsphere. A second, independent equation, based on momentum of an electron being measured as h-bar, is required to obtain a solution:
Where h-bar is Plank’s constant divided by 2 Pi, and me is the mass of an electron.
This determination of the angular momentum for a helium electron in the ground state is standard in all physics.
Between Eqs. 4-13 and 4-14 we eliminate v as a variable, and solve a single equation:
We find that r = 0.500*a0, where a0 us the Bohr radius.
The radius determined from Eq. 4-15 can be used to solve for the energy of an object in orbit, (yes, elementary rocket science) like the orbitsphere using STANDARD Maxwell equation analysis:
For helium Z=2, but Z can be any value, as discussed in the next chapter. And for Z=2, by plugging in constants we see that the solution yields -54.4 eV as the energy level of the inner electron, in agreement with the measured ionization of He+.
Once again, the GUTCP quantitative model of electron binding matches measured data exactly. The GUTCP survives a second test, with no variable parameters! As described in the preceding section, there is nothing remotely similar with SQM.
Outer Electron of Mod 1
The second electron, required to complete a neutral helium atom, approaches an ionic core in which the net electrostatic attraction is that of one proton. This is because the inner electron (-) symmetrically cancels the field of one proton (+). Hence, there is the equivalent electrostatic interaction force of only one net proton.
It must be noted, however; that unlike the first electron, which only feels the electrostatic force interaction with the protons, the second one also feels a magnetic moment.
In the GUTCP, unlike SQM, the magnetic “spin” has an actual origin: the movement of current on the surface of the orbitsphere (Ref 4-3). The magnetic force is derived from the standard form of the classical Lorentz force:
The only new variable is s, the quantum spin number, ½. Unlike with SQM, it is inherent to the structure of the orbitsphere, as described at length in the GUTCP source text.
Also, it is assumed that the outer orbitsphere is in its lowest energy state. This requires that the spin of the inner orbitsphere and the spin of the outer orbitsphere are oppositely directed, hence attractive. The opposite case, parallel spins, creates a repulsive magnetic force leading to a higher energy state, as readily verified by computation.
Thus, the magnetic force, like the Coulomb force, pulls the outer electron toward the atom center. The resulting equation for the total force felt by the outer electron and is as follows:
Note that the Coulomb force (the first term on the right side of Eq. 4-18 is the same as Eq. 4-4, except that (Z-1) is substituted for Z because effectively one nuclear charge is fully screened by the inner electron.
This equation still has two unknowns, r and v. The latter is replaced using Eq. 4-3, leading to:
For helium the Z in Eq. 4-19 is two, but as discussed in the next chapter, Z can take on any natural number value.
The value of r, computed for helium in the Mod 1 computation (Z=2) is 0.5669*a0, where a0 us the Bohr radius.
It should be noted that the net force on the outer electron is less than that on the inner electron both because it involves a net Z = 1 electrostatic force, and because the magnetic force falls off as 1/r3. This force reduction leads to the outer orbitsphere being larger than the inner orbitsphere.
Also notable is the fact that the net force on the outer electron is more than that of just one electrostatic interaction as the magnetic moment also pulls the electron in. In hydrogen there is only the single, equally large electrostatic interaction. For this reason, the outer electron of helium (0.5669*a0) is smaller than the electron of hydrogen (a0).
Now that an expression for the radius is determined, the energy of ionization can be determined.
To a first approximation, the work of ionization is equal to the work done against the electric force. It is also argued in the source text that work against the magnetic field during ionization takes place during ionization, but this is far smaller and is ignored in the first approximation.
Indeed, in this monograph this supposed magnetic work is labelled a “head scratcher,” and ignored. In any event, to the first approximation the ionization energy is obtained by integration of the first electric force term of Eq. 4-19 from r to infinity:
This leads to a binding energy of the outer electron of helium of -24.0 eV, a value nearly identical to that of the known ionization energy of the outer electron in helium.
It is notable that given the fact that both electrons have the same angular momentum, h-bar, and that there is a definitive measured relationship between electron angular momentum and magnetic moment (g-factor), both electrons will have the same magnetic moment, but opposite polarization.
Hence, as experimentally observed, ground state helium atom has no apparent net magnetic moment according to the GUTCP. The fields of the magnetic moment of the two electrons perfectly cancel.
Related: the net electric field of two protons and two spheres of charge that surround the nucleus also cancel, indicating helium should produce no electric field beyond the outer orbitsphere.23
More About Magnetic Work
In the Source Text, a fuller computation is done, which includes the magnetic energy. The magnetic work is also predictable employing classical mechanics.
Unfortunately, the algebra involved is tedious and beyond the scope of this brief introduction to the GUTCP model of helium. However, the final predicted result is simple:
Once this correction (and a small relativistic correction, ignored here) is included, the net difference between theory and prediction is a small fraction of one percent of the measured value, well within the bounds of experimental measurement error.
Why is the magnetic energy term relatively small? The electric energy term includes 1/epsilon0 and the permittivity of free space is approximately 8.85 10-12 F/m, making the first term very large.
Conclusion: The GUTCP has survived another test: it predicts the ionization energies of helium with no variable parameters, only measured constants, simple classic physics equations, and no “variational parameters.”
This outcome is utterly superior to the curve fitting routines of SQM.
Other Force Balance Considerations
A final point required: why is it that the presence of the outer electron does not modify the force balance on the inner electron? The answer involves two parts.
First, it must be noted that as the electrons never physically touch, herein called the Mod 1 Principle, the only means for the outer electron to impact the balance on the inner electron is via a field.
Second, there is neither an electric field nor a magnetic field inside a perfect superconducting cage, which is precisely the nature of an orbitsphere. No field, no effect, and no modification of the force balance.
The fact that there is no electric field inside a theoretical superconducting Faraday cage is derived from classical electromagnetic theory. The supposition that there is also no magnetic field inside a superconducting cage is based on the Meissner effect as observed for Type I superconductors.
Type I superconductors, a class to which it is postulated orbitspheres belong, completely expel internal magnetic fields.24 It is theorized this effect can be explained using classical physics alone.25
In sum:
The value of “r” is computed from the force balance using all forces.
The correct, non-approximate, value of “r” is employed to determine the work against the electric force, which to a first approximation is a good estimate of the measured ionization energy.
The PEP is rejected, and a new exclusion principle, the Mod 1 Principle is postulated: like charged particles never touch.
It is shown in the next chapter that the solved force balance equation is not only precisely predictive of helium, but also predictive of all two electron atoms (e.g. Li+). Indeed, when all small corrections are included, it is never more than 0.41% different than the measured values. Is 0.41% error a cause for concern? It is within the bounds of experimental error, but this author admits to the need for constant search for improvement.
And to repeat the basic structure: in the Mod 1 version of the GUTCP, the two electrons in helium are like a set of nested “Russian dolls,” identical except for radius and orientation of magnetic moment (Figure 4-9).
The electrons are independent three-dimensional objects that obey the same classical laws of physics just as all other objects do. The magnetic fields of the two oppositely polarized electrons cancel, as predicted by classical physics. The net electric field of the four charged species that make up helium, two protons and two spherically symmetric electrons, also cancel as predicted by classical physics.
The two electrons occupy the lowest possible energy states, per the general law that for atoms at low temperatures, the electrons are always in the lowest possible energy configuration. Higher temperature “excited states” are discussed in Ch 6.
Figure 4-9: TOP: nested bubbles of orbitspheres of a potassium according to the GUTCP model. From Source Text. BOTTOM: two-dimensional projection of the outer limits of the regions of highest probability of finding infinitely small electrons in SQM theory for orbitals with different, quantized, angular momentum.
Chapter Summary
SQM and the GUTCP are fundamentally different, thus only one can better describe observed quantum phenomenon of bound electrons. A brief summary of the fundamentals of the models follow.
SQM
SQM is based on the Schrodinger equation (1925), a model that postulates classical physics, including Newtonian physics, cannot be used to describe the behavior of elementary particles on the scale of the atom.
In the SQM model, the bound electron is an infinitely small object that jumps around, in a totally non-Newtonian fashion, that is, without trajectory. The SQM model requires a Correspondence Principle that postulates a length scale at which the world shifts from a classical physics description to a Schrodinger equation description.
Also, it does not even suggest a mechanism to explain some well-known features of bound electrons, such as magnetic moments.
Moreover, the SQM method requires tremendous computational power to curve fit a solution to anything more complex than hydrogen.
SQM does not allow for the existence of Hydrino states of hydrogen.
In brief, true SQM is a single theory, but it is never employed! Rather, computational work always requires solving one of more than a dozen approximate models. Moreover, the objective of the approximate models is to curve fit measured data. It is never the intent of these models to predict atomic spectroscopy.
Figure 4-10. From incomprehensible to incoherent. Alice Breaks the SQM Code. From Lewis Carroll, ‘Through the Looking Glass’ (1871).
GUTCP Mod 1
The GUTCP Mod 1 model describes an electron as a physical object in three dimensions that obeys classical physics laws, that is, only equations postulated before 1872 are employed. These laws are postulated to be accurate at all size scales, from universe scale to sub-atomic.
This model perfectly predicts spectroscopy of hydrogen and helium with back-of-envelope algebra. It also provides a classical physics-based explanation for many phenomena, including the magnetic moments of bound electrons.
Controversially, in addition to being consistent with all atomic spectroscopy (more on this later), the GUTCP predicts the existence of Hydrinos, a form of atomic hydrogen in which the radii of the orbitsphere is less than the Bohr radius.
For multi-electron atomic systems, Mod 1, as presented in this independent analysis, always describes electrons as three-dimensional orbitspheres that do not touch and are organized like a set of Russian dolls.
The radii of each orbitspheres are a reflection of its energy: the more tightly bound/lower energy an electron, the smaller its radius.
For example, the GUTCP model predicts, using simple algebra, the observed spectra of helium. That is, it predicts the outer electron orbitsphere has an energy of -24.59 eV, and the physically smaller inner electron orbitsphere has an energy of -54.4 eV.
This is absolutely consistent with all spectroscopic observation.
There is no energy conundrum, there is no Pauli Exclusion Principle, there is no Correspondence Principle, there is no Uncertainty. Contrast this with the completely unphysical, six dimensional, incomprehensible, mathematically intractable, SQM model of the two electrons of helium.
Occam’s Razor.
Writers note: Considering the simplicity of the above description of the ability of the GUTCP to predict atomic spectroscopy, it is interesting to reflect on this question: why do the SQM advocates want to Cancel anything and anyone who dares even to properly explain the GUTCP? How scientific! Is the community afraid of challenge?
A Mark Twain quote is relevant:
“A lie can be halfway around the world before the truth can even put its shoes on.”
Chapter 4 Personal Notes
I. I was told this story about the birth of the GUTCP model of the helium atom by a witness to all events. An expert working with a large firm interested in investing with BLP visited the BLP corporate labs. This expert had a better than average understanding of SQM and recognized SQM cannot even describe the helium atom. He asked Randy if his theory could be extended to multi-electron atoms, specifically the helium atom. To this expert, producing an accurate helium model would establish the superiority of the GUTCP over SQM. Randy answered yes, he could produce a GUTCP model of helium. Within 24 hours he had created the first legitimate, predictive, helium model. The GUTCP won.
II. The story of the end of the Pauli Exclusion Principle is not over. The continuation of this battle is one of the reasons this monograph will likely not receive the blessing of BLP.
Specifically, in the official GUTCP version of the helium atom the two electrons are spin paired, and have the same radius. This pairing even prevents independent consideration of the energy of each electron. The analysis offered in the GUTCP Source Text is different from that offered decades ago when the Mod 1 model was first developed and published in 2007 by this author (Ref 4-19).
In contrast, the above/Mod 1 analysis is unchanged over decades. The new official GUTCP version of helium can be labelled Very Complicated. The interested reader can download the GUTCP book online and actively compare it with the Mod 1 model. Look for the two-electron atom section. In the end, Occam’s Razor would suggest the Mod 1 analysis is completely consistent with observation AND with the basic premises of the GUTCP, hence is closer to the mark.
That is, the two electrons are definitively distinct with different radii, different energies, and different spin directions. There is not a shred of spectroscopic evidence to suggest otherwise. Still, it is difficult to hold a position contrary to that held by Randy without feeling a powerful UNCERTAINTY.
One outcome of this quiet debate for me is the conclusion that the GUTCP model is not, and never will be, completed. There will always be nuance and challenges.
To paraphrase Bishop Berkeley: Only God sees all. Even the greatest among us only sees a very, very small part of the whole.
In the case of the Helium debate, the tale does not have an end, but it does have a beginning. It began in ~2004, when I was working at Los Alamos National Lab in Los Alamos, New Mexico and serving about 1/3 of the time as Distinguished National Lab Professor at the University of New Mexico.
I was still working actively as a BLP consultant, wrapping up work on hydrogen line broadening in various plasmas. Randy asked me to take on an additional consulting task: verify the original GUTCP version of the two-electron atom. Prior to that all my consultant work was, like the plasma studies, designed to test experimental predictions of the GUTCP model.
I never felt I had a complete understanding of the GUTCP model, hence was happy sticking with designing and conducting experimental work with the intention of debunking it. My plan was to really study the theory after my experimental work debunked it, and I would have more time, having lost a major consulting gig.
As noted at the beginning of this book, understanding the GUTCP, given the available resources, is difficult for even the best physicist. Thus, an experimental failure to debunk was required by me before I would dedicate time for detailed study.
Never happened. Not debunked.
Thus, after more than eight years of intense and basically continuous effort on the part of myself and colleagues to debunk the predictions of the theory experimentally, and eight years of failure to do so, I decided the offer to study the theory directly using what I call “Other People’s Data” (OPD) on a consulting basis was perfect.
It was time to truly deep dive into a small bit of the GUTCP model.
I started by reviewing the GUTCP helium model. The relevant theory development section in the source text of the two-electron system was only about five pages long, but it took me weeks to work through it. Indeed, I literally sweated over it.
For this reason alone I know that those experts who claim the theory to be flawed are unlikely to have put in the time to get though even five pages. I have the book in front of me now, and its physical condition tells the story: the two sheets of the helium theory development are loose, covered with my handwritten equations/questions, and wrinkled. The book binding is broken at the point at which those two pages belong, and only that point, as well.
Unfortunately, those weeks of consideration did not lead to the outcome desired by BLP. That is, there existed an “error of interpretation” in the model, according to me. Specifically, the second electron force balance led to a different radius than the first electron force balance, but in the GUTCP text, the two electrons are assigned the same value using a “method” inconsistent with the principles of the GUTCP.
The official GUTCP model led to a series of conundrums according to this author. For example, why, given the same radius, are the two ionization energies also not the same? It is, after a fashion, the same conundrum found in SQM. To wit: if the two electrons in helium are identical, how do we explain the very different ionization energies of the first and second electrons?
This is where the Very Complicated official GUTCP model is required. The Mod 1 model is a simpler “modified” model with each electron in helium having a unique radius and energy.
My conclusion at that time: The Mod 1 GUTCP model of helium is the only model consistent with the principles of the GUTCP, as the GUTCP requires adherence to classic physics. The modified GUTCP model, as I explain in the chapter above, leads to the conclusion that the two electrons in ground state helium have different radii and very different energies.
This is completely inconsistent with the standard PEP, supposedly based on experimental work which states the two electrons are identical in every manner, including radii and energy, except for the direction of magnetic moment.
As an example, in SQM all the s-electron orbitals can have two electrons of identical energy and wave function, with one quantum number different, the spin quantum number. One is presumed spin up and the other spin down. This is not possible in Mod 1. All the orbitspheres in an atom have distinct energy, radius, etc.
How did I react to my discovery that GUTCP applied to helium forces the two helium orbitspheres to have different radii and different energies? Well, at the time it was my understanding that the data didn’t support this. I assumed the entire physics community couldn’t be composed of a herd of sheep.
For me, at that time, as “everyone knows,” the PEP was correct, and the two electrons of helium in the ground state are identical in every fashion, size, energy, etc., except for the direction of magnetic moment.
Hence, I believed the GUTCP model, properly applied, failed to match data. In short, in my mind the failure of the GUTCP to agree with the PEP debunked it.
Not surprisingly, once BLP was told I concluded the GUTCP helium model was “debunked” because it was at odds with the narrative that “everyone knows the PEP is correct,” our 12+ year consulting relationship ended.
Those familiar with the time scale of associations with BLP will recognize that 12 years is above average. In any event, I agreed that further employing me for consulting work was probably not the best use of limited resources. I never held the notion of permanent status as a consultant, so there were no hard feelings, just acceptance of a natural termination.
My working method always requires a manuscript at the termination of a project to justify and record the intense work undertaken, as per the example of this monograph. In the helium project case, I decided to write a paper regarding the modified GUTCP version of helium and to demonstrate it was inconsistent with the PEP. In other words, I planned to write a paper giving experimental proof that the GUTCP was debunked.
Given my tremendous admiration for Randy and BLP, I felt this effort must be very complete. Making it complete, it was clear to me, required a review of all the literature proving the PEP. I anticipated there would be an overwhelming amount of experimental evidence supporting the PEP, so I mentally prepared myself for many hours at the library.
After a perusal of the literature on the subject, I decided on a simple approach based on impeccable resources. The review of the PEP was to be based on three texts on multi-electron atoms, each by a different Nobel Prize winner.
The books are labelled as quantum models of multi-electron systems, but in essence close to 100% of each text is about helium, the simplest multi-electron system.
Who argues with a Nobel laureate, and who in their full senses argues with three Nobel laureates?
Problem and confusion! Studying these texts for months led to a second surprising conclusion: there is ZERO spectroscopic evidence of the PEP.
Zero.
Not only that, but the distinguished authors of those books also probably knew it. Nowhere is the energy of the two electrons of helium in the ground state explicitly stated in the text. It is not listed in any tables. Really, entire books about helium that do not include a clear statement of the ground state energy?
My interpretation of these books? They are “written around” the PEP/energy balance conundrum. After many years in the business of science writing, I know that those issues which one cannot resolve must be written around.
The closest any of these texts by Nobel Prize winners come to a statement of the original state of helium is the energy level diagram found in the H. Bethe book (Figure 4-6, above).
It is very unsatisfying from the perspective that it creates an energy conservation conundrum. If both electrons are originally at ~-24.59 eV as the diagram implies, where does the 30 eV go during the ionization of one electron, after which the other electron is clearly at -54.4 eV, etc?
Virtually all of the discussion in these books regards helium in excited states. In these states it is assumed in all the books that one electron is excited and the other at -54.4 eV.
Discussion of the state of the electrons BEFORE excitation is absolutely minimal. Discussion of the PEP is thus avoided. Coincidence?
The original plan for the article did not simply “go sideways,” it went backwards! The new theme of the manuscript, the one that was published: the GUTCP model of helium is correct, and hence the PEP is wrong. That is, I had an epiphany: in an instant I went from a skeptic of the GUTCP model to an adherent.
In that same instant I understood why SQM was and is so baffling and unsettling: SQM is nothing more than very sophisticated mathematical gibberish.
Only the GUTCP gets all of us beyond hydrogen. My earlier writings on the topic do not reflect the history of my thinking as per above, but just records my final position: Only the GUTCP provides a proper model of the helium atom, and all other atoms and derived ions as well.
III. One day at LANL during the period in which I was writing my new version of the Exclusion Principle, I found myself in an administrative office discussing the GUTCP with two high level scientists: J, who was the top protegee of former LANL Director, S.
At the time J was the chief spokesperson to the public from the lab, and many felt he was being groomed to be a future lab Director. Also present was the head of the Theoretical (T) Division of the moment, a recognized expert on quantum theory. I believe the intent was to demonstrate my ignorance of quantum, as well as the absurdity of the GUTCP, and thus justify cancelling my intended publications.
To publish at LANL one needs to pass muster with those who guard secrets, and those who like to avoid embarrassment.
My two interlocutors were clearly certain they held the scientific high ground. Per standard for the mainstream community, they assumed it is obvious they are on the rational side of the Looking Glass, and the GUTCP and its adherents are on the Bizarro side.
I took the offense-as-defense posture. I managed to thoroughly perplex both by drawing an agreed-to energy diagram for helium (like Figure 4-5) and asking, where does 29.9 eV of energy disappear to when the non-ionized electron falls from 24.59 eV to 54.4 eV?
And where, upon electron capture by the He+ ion, does that energy come from to return the electron at -54.4 eV to the -24.59 eV level? There was some babble about process dependence, which I effectively countered. Also, I fought back by asking the quantum expert to tell me the integrated value for the two-electron wave function was over all space. He insisted the value was 2. I, correctly, noted it is 1 and is 1 for any number of electrons.
I also asked for a physical interpretation of that multi-electron wave function. None was offered.
Well, the meeting went reasonably well for me. J later told me I was one of the “three smartest” scientists at the lab, while simultaneously one of the most politically naïve, and the T division head apologetically wrote that I was correct about the integrated wave function value.
In the end, I was left alone, and publication was permitted. Please peruse Ref. 4-18 and 4-19, it is truly breakthrough material!
J. C. Maxwell, A Treatise on Electricity and Magnetism, Vol. 1 and Vol. 2 (1873). *Dover reprint is of the third edition of the Treatise finished in 1891 is readily available.
I. Newton, I.B. Cohen, and A.M. Whitman, The Principia: Mathematical Principles of Natural Philosophy (1687). *A wide variety of books expounding in modern language on Newton’s Laws of Motion are available.
R.L. Mills, The Grand Unified Theory of Classical Physics, April 2023 ed. (Randell L. Mills, 2023)
N. Bohr, “LXXIII. On the constitution of atoms and molecules,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 26(155), 857–875 (1913).
P. Pearle, “Absence of radiationless motions of relativistically rigid classical electron,” Found Phys 7(11–12), 931–945 (1977).
J.S. Nodvik, “A covariant formulation of classical electrodynamics for charges of finite extension,” Annals of Physics 28(2), 225–319 (1964).
P.A.M. Dirac, “An extensible model of the electron,” Proc. R. Soc. Lond. A 268(1332), 57–67 (1962).
D. Bohm, and M. Weinstein, “The Self-Oscillations of a Charged Particle,” Phys. Rev. 74(12), 1789–1798 (1948).
H. Kragh, “Niels Bohr’s Second Atomic Theory,” Historical Studies in the Physical Sciences 10, 123–186 (1979).
A. Sommerfeld, “Zur Quantentheorie der Spektrallinien,” Annalen Der Physik 356(17), 1–94 (1916).
W. Wilson, “LXXXIII. The quantum-theory of radiation and line spectra,” The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science 29(174), 795–802 (1915).
G. H. Goedeke, ‘Classically Radiationless Motions and Possible Implications for Quantum Theory’, Phys. Rev 135, B281 (1964).
Wikipedia entry discussing the GUTCP: https://en.wikipedia.org/wiki/Brilliant_Light_Power
D. Bohm, Quantum Theory, (Prentice-Hall, Englewood Cliffs, NJ, 1951).
H. A. Bethe and E. E. Salpeter, Quantum Mechanics of One and Two-Electron Atoms, Dover Edition (Dover Publications, Mineola, NY, 2008).
L. Pauling, and E.B. Wilson, Introduction to Quantum Mechanics: With Applications to Chemistry (Dover Publications, New York, N.Y, 1985).
L. D. Landau and E. M. Lifshitz, Quantum Mechanics Non-Relativistic Theory, (Pergamon Press, Oxford, 1965).
J. Phillips, “Reconsidering the validation of multi-electron standard quantitative quantum mechanics,” Phys Essays 27(3), 327–339 (2014).
J. Phillips, “Increasing Exclusion: The Pauli Exclusion Principle and Energy Conservation for Bound Fermions Are Mutually Exclusive” Phys Essays 20, 564 (2007).
H. Eyring, J. Walter, and G.E. Kimball, Quantum Chemistry, (John Wiley and Sons, New York, 1944).
A. S. Davydov, Quantum Mechanics, (Neo Press, Peaks Island, ME, 1966).
K.H. Johnson, “Scattered Wave Theory of the Chemical Bond” in Advances in Quantum Chemistry 7, 143, (Academic Press, NY 1973).
This is electric and/or magnetic field cancelling, as opposed to social cancelling of unimportant folk by important folk.
https://www.britannica.com/science/Meissner-effect
F. London, Superfluids Vol. 1: Macroscopic Theory of Superconductivity, 2nd Ed. (Dover Publications, 1960)






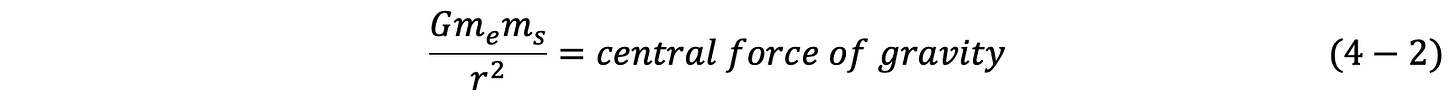
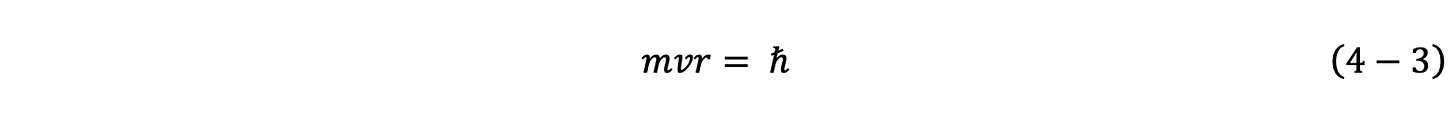













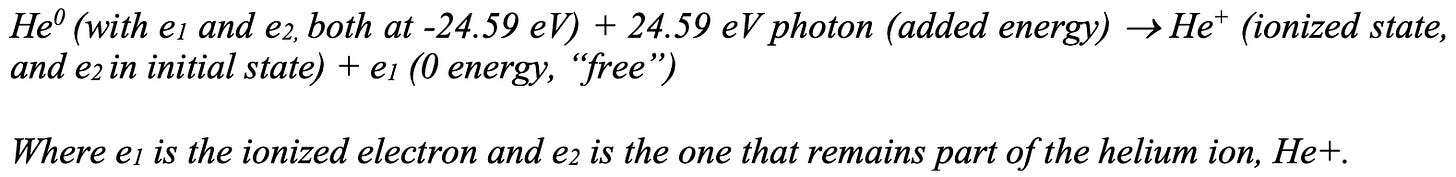








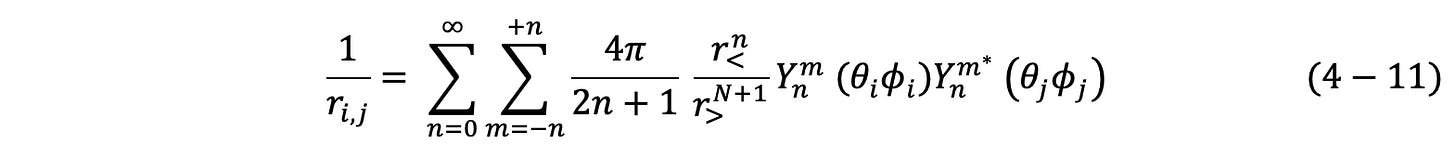




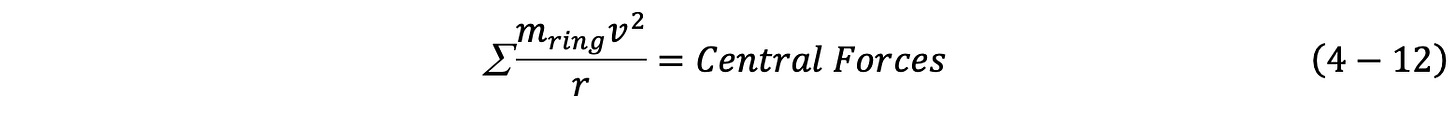











The proposal that there is no magnetic field inside the orbitsphere appears to be an essential novel element in the above interpretation of GUTCP.
Such a hypothesis strengthens the case for calculating multi-electron atoms "from the inside out", since outer electrons then have neither electrical nor magnetic influence on inner electrons. This also naturally leads to the conclusion that electrons are not 'paired' to a single radius, supporting the Mod 1 theory.
However, how would this impact the force balance of muonium (μ+e-)?
(Muonium may seem a tad exotic, but it is actually a very pure, two-orbitsphere system to test GUTCP and alternatives for basic consistency: the rules that apply to electrons should equally apply to its cousins.)
In Mills' theory, the existence of magnetic (but not electric) fields within the electron orbitsphere provides the balancing force (GUTCP eq 2.234) for the muon orbitsphere and determines its size as 9pm, with the electron radius being 53pm. What would be the driver for the muon to even curve into an orbitsphere, if it weren't for the magnetic forces of a surrounding electron?
I agree we need a GUTCP and I applaud your efforts but still have some issues. As I understand it in SQM, the electron in a Hydrogen atom is most likely to be at the Bohr radius, not at zero because that is the peak of the radial probability density. Also, regarding the issue of whether the two electrons in Helium have the same energy, that's not the issue, it's that it takes 24.6ev to ionize one of them. I don't think SQM says both electrons are at the same energy or have to be because the wavefunction is for both together. What SQM says is that the total binding energy is ~ -79ev. And yes, one has to jump through hoops to get anywhere close with SQM.
Any version of GUTCP must also explain the ordering and filling of electron levels of multi-electron atoms and be consistent with the spectroscopic data. How do you align your model with S,P, D and F states? Do you predict the same order of filling higher states that Dr. Mills and SQM for that matter?
Finally, I was really hoping you would be able to help us understand how to compute the magnetic forces for multi-electron atoms as Mills' text is hard to follow why the different magnetic forces exist for different electron atoms. For example, why the magnetic forces for 17 electron atoms is different than 18 electron atoms and how to generate them in a consistent and logical way either for Mills' version or yours. Thanks.